[백준] 32168 완전 이진 트리와 쿼리

작성일 In , Views: Disqus:

문제 링크 : https://www.acmicpc.net/problem/32168

풀이 및 구현

1번 정점이 루트인 완전 이진 트리에서 두가지 쿼리를 처리해야 한다.

  1. 트리의 루트를 v로 바꾸기
  2. 현재 트리에서 v정점 서브 트리에 있는 모든 정점 번호의 합을 출력하기

정점의 개수가 $(1 \leq N \leq 10^9)$ 이기 때문에 탐색으로는 풀 수 없다.

그래서 정점이 바뀔 때 트리에서 일어나는 일을 관찰해보았다.

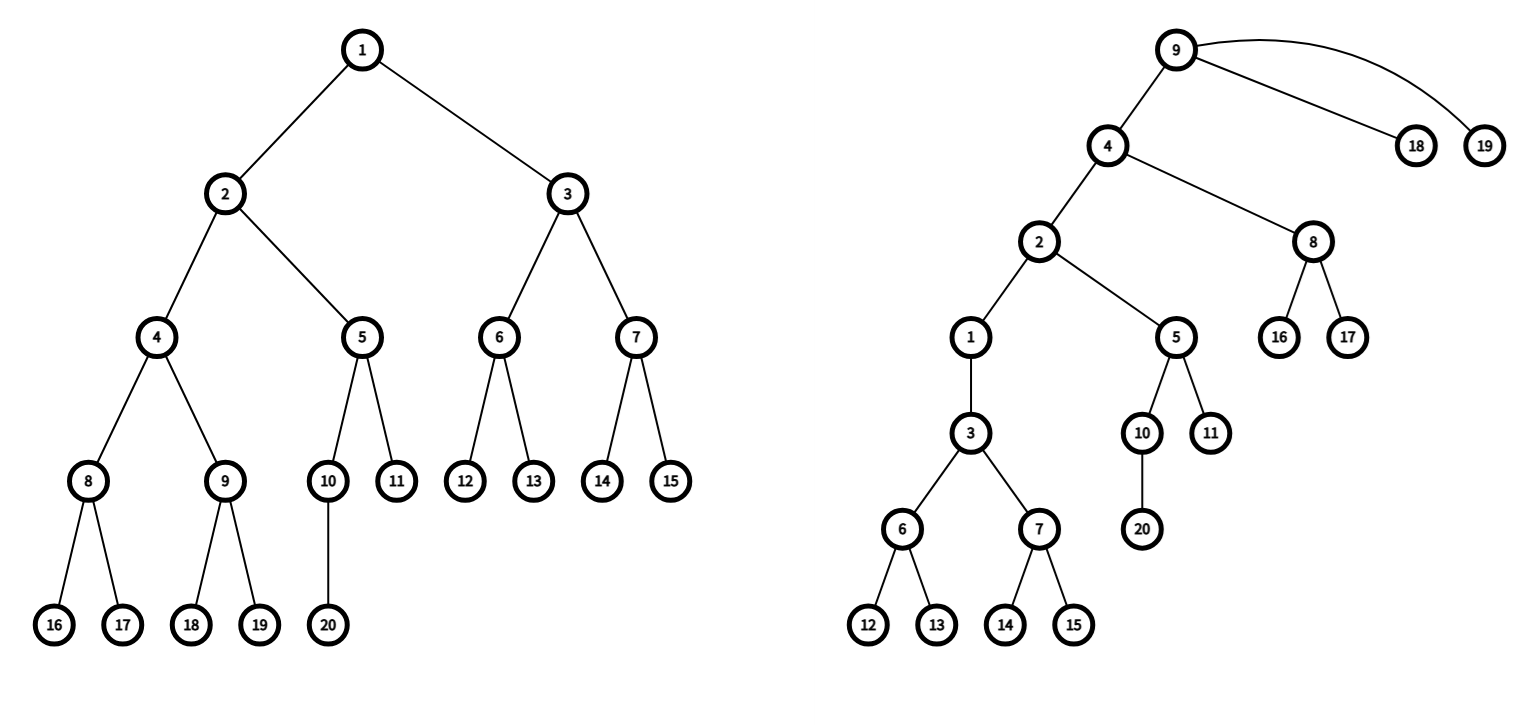
img.png

루트가 1일 때 완전 이진 트리와 루트를 9로 바꿨을 때 완전 이진 트리이다.

이때 서브 트리가 바뀐 정점들을 찾아보면 1번 정점, 2번 정점, 4번 정점 그리고 9번 정점이다.

4개 정점의 공통점은 루트가 1인 완전 이진 트리에서 9번 정점을 서브 트리에 포함하고 있는 정점들이다.

이를 일반화 하면 v정점의 서브 트리의 합이 바뀌는 경우는 현재 트리의 루트 정점이 원래 v정점의 서브 트리에 포함되어 있는 경우이다.

그래서 2번 쿼리가 들어오면 현재 루트 정점과 v정점가 원래 완전 이진 트리에서 어떤 관계를 가졌는지 확인하고 그에 맞게 합을 계산하면 된다.

경우의 수는 총 4가지가 나온다.

  1. 루트 정점이 v정점 기존의 서브 트리에 포함되지 않을 때
    • 서브 트리에 변화가 없으므로 그냥 합을 구하면 된다.
  2. 루트 정점이 v정점 기존의 왼쪽 서브 트리에 포함 될 때
    • 2번 노드의 경우이다. 전체 정점 번호의 합 - 왼쪽 서브 트리 정점 번호의 합으로 구할 수 있다.
  3. 루트 정점이 v정점 기존의 오른쪽 서브 트리에 포함될 때
    • 4번 노드의 경우이다. 전체 정점 번호의 합 - 오른쪽 서브 트리 정점 번호의 합으로 구할 수 있다.
  4. 루트 정점과 v정점이 동일 할 때
    • 전체 노드의 합을 구하면 된다.

이를 구현하기 위해 우선 v정점 서브 트리의 합을 구하는 코드를 만들었다.

$x$번 정점이 $\lfloor \frac x2 \rfloor$번 정점을 부모로 가지므로 이 규칙을 활용해 합을 쉽게 구할 수 있다.

왼쪽은 항상 번호가 2배가 되고 오른쪽의 번호는 항상 2배 + 1로 커진다.

또한 같은 높이에서는 정점의 번호가 연속되므로 양 끝을 범위 합을 이용해 한 높이씩 훑어 가면 된다.

완전 이진 트리의 높이는 $log_2{N}$ 이므로 연산마다 최대 30번정도 훑어 매번 계산해도 상관없다.

2번 정점의 서브 트리를 구할 때는 아래 그림처럼 구하게 된다.

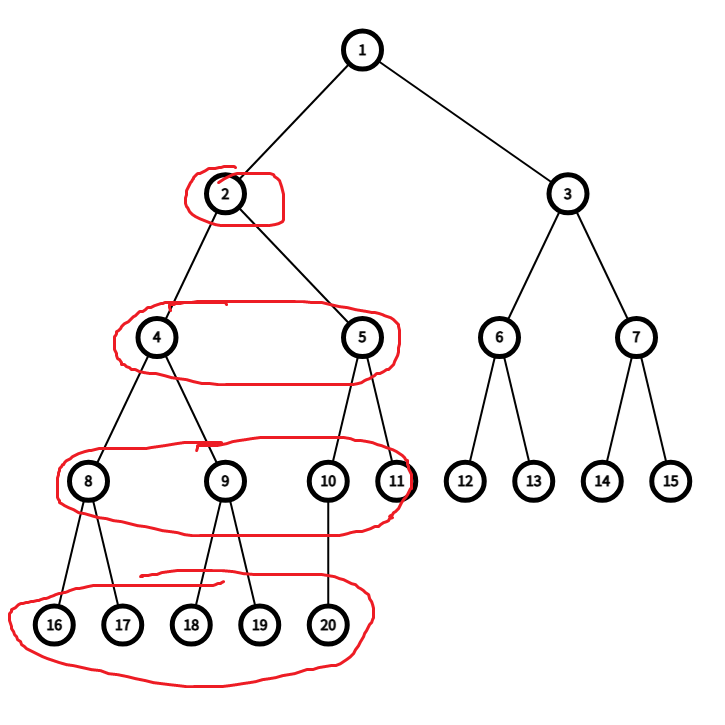
img_1.png

이를 함수로 구현해서 사용했다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
long long get_sum(long long N, long long v) {
    // 범위를 벗어난 입력이 들어올 때
    if (v > N) return 0;
    
    // 자신도 포함한다.
    auto sum = v;
    
    // 서브 트리의 양 끝 값을 계산
    auto l = v << 1, r = (v << 1) + 1;
    
    // 전체 노드의 범위동안만 계산 
    while (l <= N) {
        // 오른쪽 노드가 범위를 벗어날 수 있으므로 보정
        r = min(r, N);
        
        // 범위 합
        sum += (r - l + 1) * (r + l) / 2;
        
        // 한 칸 내려간다.
        l = l << 1;
        r = (r << 1) + 1;
    }
    return sum;
}

다음은 두 정점의 관계를 계산하는 함수를 만들었다.

서브 트리가 바뀌는 경우인 현재 트리의 루트 정점이 원래 v정점의 서브 트리에 포함되어 있는 경우를 찾아야 하므로 루트 정점을 점점 올리면서 v정점과 만나는 경우가 있는지 확인했다.

4가지 경우의 수가 있으므로 각 경우마다 다른 값을 리턴해주었다.

  • 0: v정점을 만나지 않은 경우 서브 트리에 포함되지 않는다.
  • 1: 왼쪽 서브 트리에 포함된 경우
  • 2: 오른쪽 서브 트리에 포함된 경우
  • 3: 루트 정점과 v정점이 동일한 경우
1
2
3
4
5
6
7
8
int find(long long r, long long v) {
    if (r == v) return 3;
    while (r > 1) {
        if (r >> 1 == v) return r % 2 + 1;
        r >>= 1;
    }
    return 0;
}

1번 쿼리가 들어오면 현재 루트의 번호만 저장하고 2번 쿼리가 들어오면 find 함수를 이용해 관계를 알아낸 뒤 경우의 수에 따라 처리하면 된다.

전체 합은 미리 sum 변수에 1번 정점의 서브 트리 합으로 구해 놓고 사용했다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 전체 합
auto sum = get_sum(N, 1);

// 현재 루트의 번호
long long root = 1;

for (int i = 0; i < M; i++) {
    int q, v; cin >> q >> v;
    
    // 1번 쿼리에서는 루트만 변경한다.
    if (q == 1) {
        root = v;
    }
    else {
    
        // 루트 정점과 v정점의 관계를 확인하고 각 경우에 따라 처리한다.
        int result = find(root, v);
        if (!result) cout << get_sum(N, v) << '\n';
        else if (result == 1) {
            cout << sum - get_sum(N, v * 2) << '\n';
        }
        else if (result == 2) {
            cout << sum - get_sum(N, v * 2 + 1) << '\n';
        }
        else {
            cout << sum << '\n';
        }
    }
}

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
using namespace std;

long long get_sum(long long N, long long v) {
    if (v > N) return 0;
    auto sum = v;
    auto l = v << 1, r = (v << 1) + 1;
    while (l <= N) {
        r = min(r, N);
        sum += (r - l + 1) * (r + l) / 2;
        l = l << 1;
        r = (r << 1) + 1;
    }
    return sum;
}

int find(long long r, long long v) {
    if (r == v) return 3;
    while (r > 1) {
        if (r >> 1 == v) return r % 2 + 1;
        r >>= 1;
    }
    return 0;
}

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    long long N, M;
    cin >> N >> M;

    auto sum = get_sum(N, 1);
    long long root = 1;
    for (int i = 0; i < M; i++) {
        int q, v; cin >> q >> v;
        if (q == 1) {
            root = v;
        }
        else {
            int result = find(root, v);
            if (!result) cout << get_sum(N, v) << '\n';
            else if (result == 1) {
                cout << sum - get_sum(N, v * 2) << '\n';
            }
            else if (result == 2) {
                cout << sum - get_sum(N, v * 2 + 1) << '\n';
            }
            else {
                cout << sum << '\n';
            }
        }
    }
}

후기

img_2.png

4번째 경우인 루트 = v 경우를 잘못 처리해서 3번이나 틀렸다.

처음엔 그냥 4번째 경우를 1번째 경우와 동일하게 처리했다. 그래서 처음 틀렸을 때 오버플로우 문제인가 하면서 다른 곳들을 고쳤어서 2번을 더 틀렸었다.

그런데 다시 생각해 보니 동일하면 전체 합을 출력해야 한다는 것을 깨달아 맞출 수 있었다.