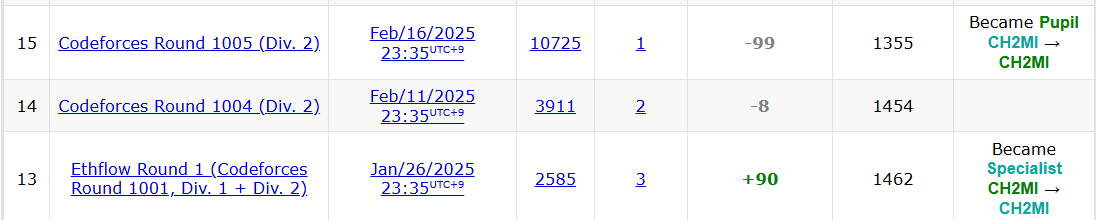
[Codeforces] Codeforces Round 1031 (Div. 2) 후기

작성일 In , Views: Disqus:

지난 글 이후로 겨울 동안 코드포스를 조금씩 했었는데 민트를 찍자마자 다시 떨어졌다.

그 뒤로 더 떨어질 것 같다는 생각에 한동안 하지 않았다.

img_1.png

막연하게 코드포스 블루를 언제 다시 도전할지 생각만 하고 있을 때쯤 이번 라운드가 18시 05분 시작이었다.

종강도 했고 잃어버린 감각을 되찾다는 느낌으로 2솔을 목표로 이번 라운드에 참가했다.

img.png

Contest 링크 : Codeforces Round 1031 (Div. 2)

A. Shashliks

한 줄에 $k, a, b, x, y$가 주어진다.

두가지 요리가 있는데 첫번째 요리는 온도가 $a$ 이상일 때 요리할 수 있고 온도를 $x$만큼 감소시킨다.

두번째 요리는 온도가 $b$ 이상일 때 요리할 수 있고 온도를 $y$만큼 감소시킨다.

초기 온도가 $k$도일 때 요리할 수 있는 최대 횟수를 구하는 문제이다.

요리를 최대한 많이 해야 하므로 온도 감소가 적은 요리를 더 많이 하면 된다.

따라서 $x$와 $y$를 비교하고 온도 감소가 더 적은 쪽의 요리를 최대한 많이 만든 후 남은 온도로 다른 요리를 하면 된다.

이때 반복해서 빼기로 연산하면 TLE가 날 수 있기 때문에 나누기로 횟수를 세어주었다.

코드 보기 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
using namespace std;

void solve() {
    int k, a, b, x, y;
    cin >> k >> a >> b >> x >> y;

    int cnt = 0;
    if (x < y) {
        if (k >= a) {
            int t = (k - a) / x;
            cnt += t + 1;
            k -= (t + 1) * x;
        }
        if (k >= b) {
            int t = (k - b) / y;
            cnt += t + 1;
            k -= (t + 1) * y;
        }
    }
    else {
        if (k >= b) {
            int t = (k - b) / y;
            cnt += t + 1;
            k -= (t + 1) * y;
        }
        if (k >= a) {
            int t = (k - a) / x;
            cnt += t + 1;
            k -= (t + 1) * x;
        }
    }
    cout << cnt << '\n';
}

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int T; cin >> T;
    while (T--) {
        solve();
    }
}

B. Good Start

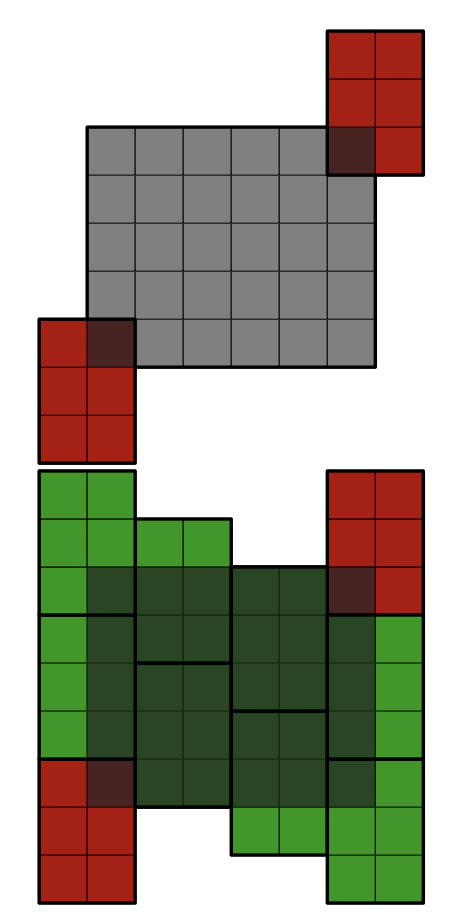
$w * h$ 크기의 직사각형과 $a * b$ 크기의 직사각형이 주어지고 $a * b$ 직사각형 2개의 좌표가 주어진다.

$a * b$ 직사각형들로 $w * h$ 직사각형을 빈틈없이 덮어야 하는데 $a * b$ 직사각형을 회전시키면 안되고, 다른 $a * b$ 직사각형과 겹치게 놓으면 안된다.

이미 놓여진 2개의 $a * b$ 직사각형의 위치는 고정일 때 $a * b$ 직사각형을 더 추가해서 $w * h$를 덮을 수 있는지 판단하는 문제이다.

아래 그림을 보면 빨간색 직사각형이 이미 놓여진 $a * b$ 직사각형이고 여러 개를 더 추가하여 $w * h$ 직사각형을 다 덮었다.

img_2.png

하지만 이 경우에는 어떠한 방법으로도 덮을 수 있는 방법이 없다.

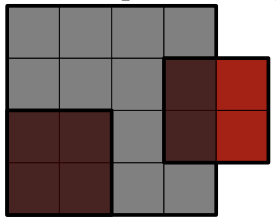
img_3.png

$w * h$ 직사각형을 다 덮기 위해서는 두 직사각형 사이의 간격이 변의 길이의 배수가 되어야 한다.

회전할 수 없기 때문에 두 직사각형의 $x$좌표 차이가 $a$의 배수이거나 $y$좌표 차이가 $b$의 배수여야 한다.

만약 둘다 배수가 아니면 덮을 수 없지만 하나라도 맞으면 덮을 수 있다.

다만 한 방향으로 좌표 차이가 0일 때는 다른 쪽이 배수이어야 덮을 수 있다.

그래서 두 직사각형 위치에 따라 경우의 수를 나누어 배수 판별을 해주면 된다.

코드 보기 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
using namespace std;

void solve() {
    long long w, h, a, b, x1, y1, x2, y2;
    cin >> w >> h >> a >> b >> x1 >> y1 >> x2 >> y2;

    if (x1 < x2) {
        if (y1 < y2) {
            if ((y2 - (y1 + b)) % b && (x2 - (x1 + a)) % a) cout << "NO";
            else cout << "YES";
        }
        else if (y2 < y1) {
            if ((y1 - (y2 + b)) % b && (x2 - (x1 + a)) % a) cout << "NO";
            else cout << "YES";
        }
        else {
            if ((x2 - (x1 + a)) % a) cout << "NO";
            else cout << "YES";
        }
    }
    else if (x2 < x1){
        if (y1 < y2) {
            if ((y2 - (y1 + b)) % b && (x1 - (x2 + a)) % a) cout << "NO";
            else cout << "YES";
        }
        else if (y2 < y1) {
            if ((y1 - (y2 + b)) % b && (x1 - (x2 + a)) % a) cout << "NO";
            else cout << "YES";
        }
        else {
            if ((x1 - (x2 + a)) % a) cout << "NO";
            else cout << "YES";
        }
    }
    else {
        if (y1 < y2) {
            if ((y2 - (y1 + b)) % b) cout << "NO";
            else cout << "YES";
        }
        else if (y2 < y1) {
            if ((y1 - (y2 + b)) % b) cout << "NO";
            else cout << "YES";
        }
        else cout << "YES";
    }
    cout << '\n';
}

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int T; cin >> T;
    while (T--) {
        solve();
    }
}

4번 WA가 나왔는데 else if에서 조건문을 보면 괄호가 하나 비어 있어서 틀린 것이다.

img_4.png

저 부분을 눈치채지 못해서 계속해서 WA가 나와 맞왜틀을 외치다가 겨우 발견했다.

그런데 (y2 - (y1 + b)) % b는 사실 (y2 - y1) % b와 동일한 식이다.

긴장해서 그런지 복잡하게 생각해서 앞의 식으로 사용했는데 라운드 끝나고 에디토티얼을 보면서 복잡하게 생각했다는 것을 깨달았다.

처음부터 저렇게 조건문을 구성했다면 WA가 4번 나오지 않았을 것이다…

C. Smilo and Minecraft

$n * m$크기에 빈 땅, 돌, 금이 있다.

빈 땅에 TNT을 놓아 터트릴 수 있는데 TNT를 중심으로 한 변의 길이가 $2K - 1$인 정사각형 내부에 있는 모든 곳을 빈 땅으로 만들어 버린다.

그리고 폭발의 범위와 맞닿아 있는 부분의 금을 가져갈 수 있다.

아래 예시를 보면 TNT의 폭발력이 2일 때 폭발이 만드는 정사각형 길이는 3이 되고 두번째에서 그림에서 이와 맞닿아 있는 부분의 금 2개를 가져갈 수 있다.

이후 TNT를 한번 더 터트려 남은 금 2개도 가져갈 수 있다.

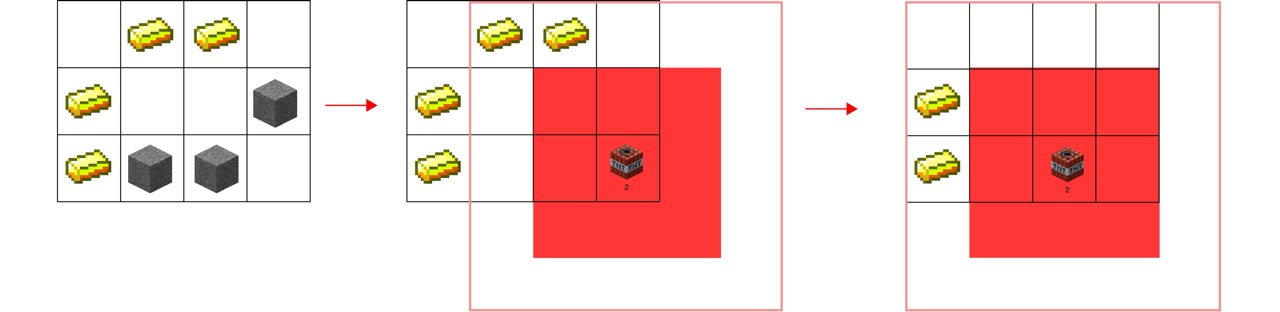
img_5.png

TNT를 여러번 터트릴 수 있을 때 최대한 많이 금을 몇 개 가져가야 하는지 구해야 한다.

처음에 든 생각은 백트래킹으로는 절대 풀 수가 없는데 어떻게 접근할지 의문이 들었다.

그래서 저 사진 처럼 직사각형의 꼭짓점 근처부터 터트리면 최대한 손실 없이 가져갈 수 있다고 생각했는데 꼭짓점 쪽에 빈 칸이 없으면 이 방법도 무용지물이다.

여기서 떠오른 것은 처음 폭발을 일으키면 외곽부분의 금을 모두 회수하기 때문에 그 다음부터는 외곽부분이 폭발 범위에 있어도 괜찮다는 것이다.

즉 처음 폭발 때 금을 최소한으로 잃으면 남아있는 금을 모두 가져갈 수 있다.

따라서 빈 칸에 TNT를 한 번씩 놓아보면서 몇 개 잃는 지 계산한 후 전체 금의 개수 - 최소로 잃는 금의 개수를 계산하면 된다.

$k$의 범위가 $(1 \leq k \leq 500)$이므로 매 위치마다 주변을 탐색하긴 힘들기 때문에 2차원 누적합을 활용해 미리 금의 개수를 미리 저장해 놓고 매 위치마다 계산하면 된다.

정리해보면

  1. 2차원 누적합으로 금의 개수를 저장한다.
  2. 빈칸을 돌면서 TNT로 잃는 금의 최솟값을 계산한다.
  3. 전체 금의 개수에서 최솟값을 빼어 최대로 얻을 수 있는 금의 개수를 계산한다.
코드 보기 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;

void solve() {
    int n, m, k;
    cin >> n >> m >> k;

    vector<string> v(n);
    for (auto& s : v) cin >> s;

    int cnt = 0;
    vector<vector<int>> ps(n + 1, vector<int>(m + 1));
    
    // 금의 개수를 누적합으로 저장
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            ps[i][j] = (v[i - 1][j - 1] == 'g') + ps[i - 1][j] + ps[i][j - 1] - ps[i - 1][j - 1];
            cnt += v[i - 1][j - 1] == 'g';
        }
    }

    int mn = n * m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            
            // 각 빈 칸에서 TNT를 터트렸을 때 금을 몇 개 잃는지 계산하고 최솟값을 저장
            if (v[i][j] == '.') {
                int x1 = max(0, i - k + 1) + 1, y1 = max(0, j - k + 1) + 1;
                int x2 = min(n - 1, i + k - 1) + 1, y2 = min(m - 1, j + k - 1) + 1;

                mn = min(mn, ps[x2][y2] - ps[x1 - 1][y2] - ps[x2][y1 - 1] + ps[x1 - 1][y1 - 1]);
            }
        }
    }

    cout << cnt - mn << '\n';
}

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int T; cin >> T;
    while (T--) {
        solve();
    }
}

평소 배열 저장은 0-base로 하고 누적합은 1-base로 하다보니 이를 변환할 때 머리가 꼬여서 제대로 계산이 되지 않았다.

이 부분에서 디버깅만 30분 걸린 것 같다. 그래서 시간이 점점 줄어들수록 초조해졌는데 다행히 풀 수 있었다.

D. Cheater , E. From Kazan with Love , F. Two Arrays

C번을 푼 시점에서 8분 정도 남아 있어서 라운드를 마무리 했다.

후기

img_6.png
원래 목표가 2문제였는데 3문제를 풀었다.

B번에서 WA만 4번 나올 때 오늘 라운드도 점수가 떨어지겠다 싶었는데 다행히 C번을 풀어 점수가 올랐다.

B번에서 괄호만 잘 봤으면 점수가 훨씬 더 좋았을 것 같다.

그리고 이번 라운드를 통해 무사히 민트를 복구했다.

img_7.png