[백준] 17371 이사 (C++)

문제 링크 : https://www.acmicpc.net/problem/17371

풀이 및 구현

$N$개의 편의시설이 주어질 때 어떤 좌표에서 가장 가까운 편의시설까지의 거리와 가장 먼 편의시설까지의 거리의 평균이 최소가 되도록 하는 어떤 좌표를 찾는 문제이다.

주어진 편의시설의 개수가 최대 $10^3$개이므로 가장 먼 편의시설과 가장 가까운 편의시설을 고정하고 브루트포스로 돌려서 해결할 수 있다고 생각했다.

하지만 두 점을 정했을 때 두 점 사이에서 어떻게 이사할 좌표를 정할지 아이디어가 떠오르지 않아 예제 입력을 직접 그림으로 그려보았다.

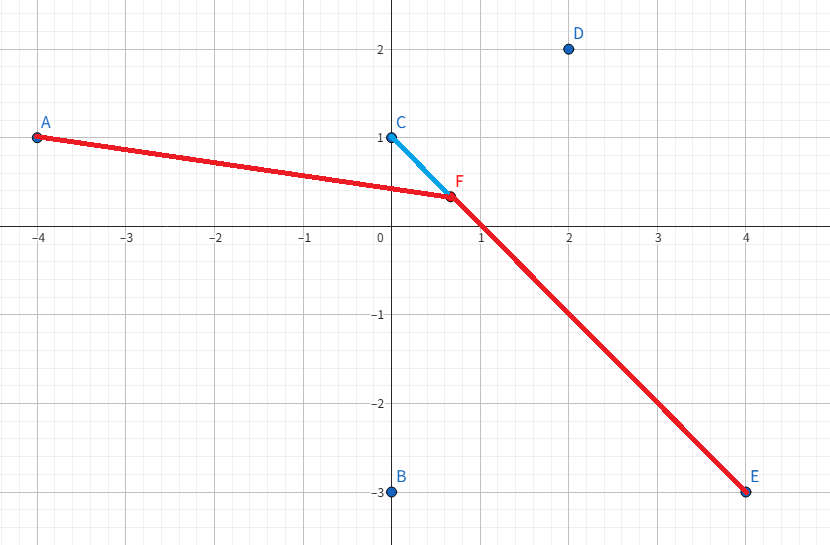
이사할 좌표의 위치를 점 $F$라고 하면 점 $F$에서 가장 가까운 편의시설은 점 $C$이고 가장 먼 편의시설은 점 $A$와 점 $E$이다.

이때 점 $F$는 선분 $CE$위에 존재하는데 점 $F$가 선분 위에서 움직이더라도 선분$CF$의 길이와 선분 $EF$의 길이의 평균은 변하지 않는다.

선분 위의 점 $F$에 대해 $|CF| + |FE| = |CE|$이므로 $\frac{|CF| + |FE|}{2} = \frac{|CE|}{2}$ 이다. 따라서 평균이 항상 $\frac{|CE|}{2}$로 유지된다.

즉 점 $F$의 위치를 점 $C$나 점 $E$에 놓아 가장 가까운 편의시설까지의 거리를 0으로 설정해도 가장 먼 편의시설까지의 거리와의 평균은 변하지 않는다.

따라서 각 점에서 가장 먼 편의시설까지의 거리를 계산한 뒤 가장 먼 편의시설까지의 거리가 최소가 되는 점을 찾으면 된다.

거리 계산은 유클리드 거리를 사용하는데 크기 비교에만 사용하면 되므로 혹시 모를 오차를 대비해 계산 결과에 루트를 씌우지 않았다.

typedef array<double, 2> point;

double getDist(point& a, point& b) {
    return (a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]);
}

그리고 브루트포스로 각 점에 대해 제일 먼 거리를 구한 뒤 최솟값을 갖는 점을 구하면 된다.

for (int i = 0; i < N; i++) {
    for (int j = 0; j < N; j++) {
        dist[i] = max(dist[i], getDist(v[i], v[j]));
    }
}

point ans = v[min_element(dist.begin(), dist.end()) - dist.begin()];

코드

#include <bits/stdc++.h>
using namespace std;

typedef array<double, 2> point;

double getDist(point& a, point& b) {
    return (a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]);
}

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);

    int N; cin >> N;
    vector<point> v(N);
    for (auto& [x, y] : v) cin >> x >> y;

    vector<double> dist(N);
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            dist[i] = max(dist[i], getDist(v[i], v[j]));
        }
    }

    point ans = v[min_element(dist.begin(), dist.end()) - dist.begin()];
    cout << ans[0] << ' ' << ans[1];
}

후기

$N$의 범위에서 힌트를 얻었고 그림을 그려보니 바로 풀이법이 보인 문제였다.

그림을 그리지 않았다면 주어진 예제 때문에 더 어려웠을 것 같다.