[백준] 1948 임계경로 (C++)

작성일 In , Views: Disqus:

문제

원문 링크 : https://www.acmicpc.net/problem/1948

월드 나라는 모든 도로가 일방통행인 도로이고, 싸이클이 없다. 그런데 어떤 무수히 많은 사람들이 월드 나라의 지도를 그리기 위해서, 어떤 시작 도시로부터 도착 도시까지 출발을 하여 가능한 모든 경로를 탐색한다고 한다.

이 지도를 그리는 사람들은 사이가 너무 좋아서 지도를 그리는 일을 다 마치고 도착 도시에서 모두 다 만나기로 하였다. 그렇다고 하였을 때 이들이 만나는 시간은 출발 도시로부터 출발한 후 최소 몇 시간 후에 만날 수 있는가? 즉, 마지막에 도착하는 사람까지 도착을 하는 시간을 의미한다.

어떤 사람은 이 시간에 만나기 위하여 1분도 쉬지 않고 달려야 한다. 이런 사람들이 지나는 도로의 수를 카운트 하여라.

출발 도시는 들어오는 도로가 0개이고, 도착 도시는 나가는 도로가 0개이다.

풀이 및 구현

문제 시작에서 모든 도로가 일방통행이고, 싸이클이 없다고 했기 때문에 도로로 만들 수 있는 그래프는 방향 비순환 그래프, DAG가 된다.

DAG하면 제일 먼저 떠오르는 것은 위상정렬이기 때문에 위상정렬을 사용하는 쪽으로 문제를 접근했다.

출발 도시에서 시작해서 도착 도시에 모두 모이는 데 걸리는 시간을 계산해야 하므로 출발 도시에서 도착 도시까지의 최장 경로를 구하면 된다.

위상 정렬을 할 때 어떤 정점이 큐에 들어가기 위해서는 해당 정점으로 들어가는 간선에 대해 모두 계산이 완료되어야 한다. 즉 큐에 들어가는 순간 출발 정점에서 해당 정점까지 가는 모든 경로가 탐색되었으니 그 중에서 최댓값을 관리하고 있으면 된다.

vector<pair<int, vector<int>>> arr(n);

각 정점에 대한 정보를 위와 같은 형식으로 관리했다.

int는 출발 정점에서 해당 정점까지가는 최장 경로를 의미한다.

vector<int>는 추후 설명할 역추적을 위해 필요하며 이전 정점을 관리하고 있다.

1
2
3
4
5
6
7
8
9
10
11
12
q.push(s);
while (!q.empty()) {
        int cur = q.front();
        q.pop();

        for (auto& [nxt, w] : adj[cur]) {
            if (!--indegree[nxt]) q.push(nxt);
            if (arr[cur].first + w > arr[nxt].first) {
                arr[nxt].first = arr[cur].first + w;
            }
        }
    }

위의 위상정렬 코드에서 nxt 정점까지 가는 경로보다 cur 정점에서 이동하는 경로가 클 때 최댓값 갱신을 해주면 위상 정렬이 완료되었을 때 각 정점까지의 최장 경로를 구할 수 있다.

다음으로 할 일은 최장 경로를 구했을 때 최장 경로로 가기 위한 도로의 수를 구해야 한다.

도로의 수가 어떤 것을 의미하는 것인지 잘 이해가 안될 수도 있는데 아래 예제를 보면 쉽게 알 수 있다.

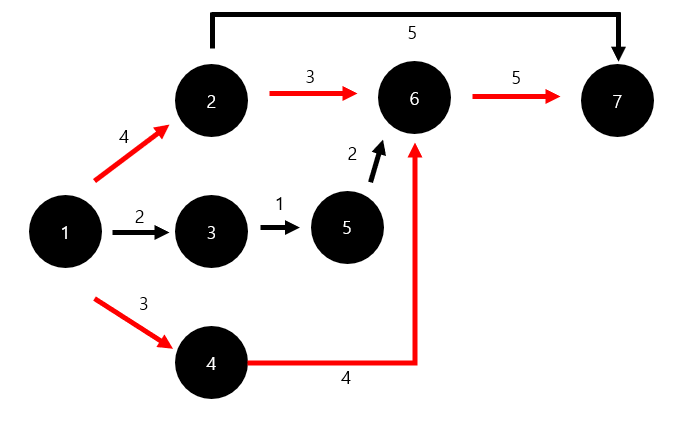
alt text

1 -> 7로 가기 위한 최장 경로는 12이고, 1 -> 2 -> 6 -> 7과 1 -> 4 -> 6 -> 7 두 개의 경로가 있다. 이 때 6 -> 7 도로는 두 경로에서 공통적으로 사용하기 때문에 최장 경로에 필요한 도로의 개수는 총 5개이다.

최장 경로를 저장할 때 해당 최장 경로가 어떤 정점에서 왔는지 저장하고, 위상정렬이 끝난 후에 이를 역추적하면 쉽게 개수를 구할 수 있다.

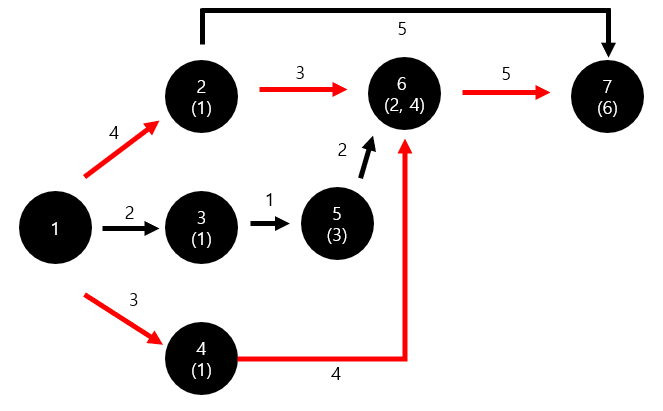
alt text

위의 그림과 같은 방법으로 최장 경로가 되는 이전 노드를 저장하면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
q.push(s);
while (!q.empty()) {
        int cur = q.front();
        q.pop();

        for (auto& [nxt, w] : adj[cur]) {
            if (!--indegree[nxt]) q.push(nxt);
            if (arr[cur].first + w > arr[nxt].first) {
                arr[nxt].first = arr[cur].first + w;
                arr[nxt].second = {cur};
            }
            else if (arr[cur].first + w == arr[nxt].first) {
                arr[nxt].second.push_back(cur);
            }
        }
    }

이를 바탕으로 위상정렬 코드를 다시 구성했다.

vector<pair<int, vector<int>>> arr(n); 에서 vector<int>부분이 바로 이를 위한 것이다.

if (arr[cur].first + w > arr[nxt].first) 이 경우에는 최댓값이 갱신될 때이므로 arr[nxt].second 에는 cur만 저장해준다.

else if (arr[cur].first + w == arr[nxt].first) 이 경우에는 기존 최댓값과 현재 최댓값이 동일한 경우인데 모든 최장 경로에 대해 확인해야하므로 cur을 추가해주었다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int cnt = 0;
    vector<int> visited(n);
    q.push(e);
    while (!q.empty()) {
        int cur = q.front();
        q.pop();

        if (visited[cur]) continue;
        visited[cur] = 1;
        for (int& nxt : arr[cur].second) {
            q.push(nxt);
            cnt++;
        }
    }

위상정렬이 끝나고 위와 같이 역추적을 해주면 도로의 개수를 알 수 있다.

visited 배열의 경우 한 노드의 진출 차수 중 2개 이상이 최장 경로에 해당되면 역추적할 때 2번 이상 뽑힐 수 있기 때문에 중복 검사가 필요하다.

최장 경로에 포함되는 정점에 대해 미리 저장해 놓은 직전 노드의 개수를 세면 최장 경로에 포함되는 모든 도로의 개수를 셀 수 있다.

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <bits/stdc++.h>
using namespace std;

int n;
vector<vector<array<int, 2>>> adj;

void Topology_sort(int s, int e) {
    vector<int> indegree(n);
    vector<pair<int, vector<int>>> arr(n);
    queue<int> q;
    for (int i = 0; i < n; i++) {
        for (auto& [e, w] : adj[i]) indegree[e]++;
    }
    q.push(s);

    while (!q.empty()) {
        int cur = q.front();
        q.pop();

        for (auto& [nxt, w] : adj[cur]) {
            if (!--indegree[nxt]) q.push(nxt);
            if (arr[cur].first + w > arr[nxt].first) {
                arr[nxt].first = arr[cur].first + w;
                arr[nxt].second = {cur};
            }
            else if (arr[cur].first + w == arr[nxt].first) {
                arr[nxt].second.push_back(cur);
            }
        }
    }

    cout << arr[e].first << '\n';
    int cnt = 0;
    vector<int> visited(n);
    q.push(e);
    while (!q.empty()) {
        int cur = q.front();
        q.pop();

        if (visited[cur]) continue;
        visited[cur] = 1;
        for (int& nxt : arr[cur].second) {
            q.push(nxt);
            cnt++;
        }
    }
    cout << cnt;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);

    int m;
    cin >> n >> m;

    adj.assign(n, vector<array<int, 2>>());

    while(m--) {
        int s, e, w;
        cin >> s >> e >> w;
        adj[s - 1].push_back({e - 1, w});
    }

    int s, e; cin >> s >> e;
    Topology_sort(s - 1, e - 1);
}

후기

alt text

위상정렬한 뒤 역추적 아이디어가 정말 좋았던 문제이다.

단순하게 계산하면 한 정점에서 갈라졌다가 이후 정점에서 합쳐지는 경로가 모두 최장 경로일 때 문제가 생길 수 있으니 조심해야 한다.