[백준] 4095 최대 정사각형 (C++)

문제

원문 링크 : https://www.acmicpc.net/problem/4095

1과 0으로 이루어진 NxM크기의 행렬이 주어졌을 때, 1로만 이루어진 가장 큰 정사각형 부분 행렬 찾는 프로그램을 작성하시오.

풀이 및 구현

다이나믹 프로그래밍을 이용하면 쉽게 풀 수 있다.

$N * M$크기의 dp 배열을 만들고, dp[i][j]의 의미를 $A_{ij}$를 정사각형의 우측 하단 꼭지점으로 했을 때 만들어지는 최대 정사각형의 크기라고 생각하면 된다.

1번 테스트 케이스로 예시로 들면 아래와 같다.
왼쪽이 입력값과 만들어지는 정사각형이고 오른쪽이 dp 배열일 때 정사각형의 크기마다 그림으로 그려보았다.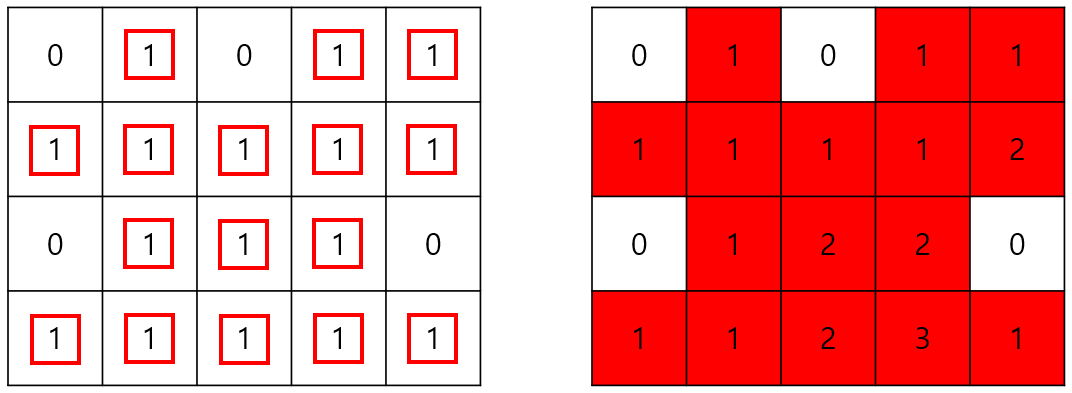

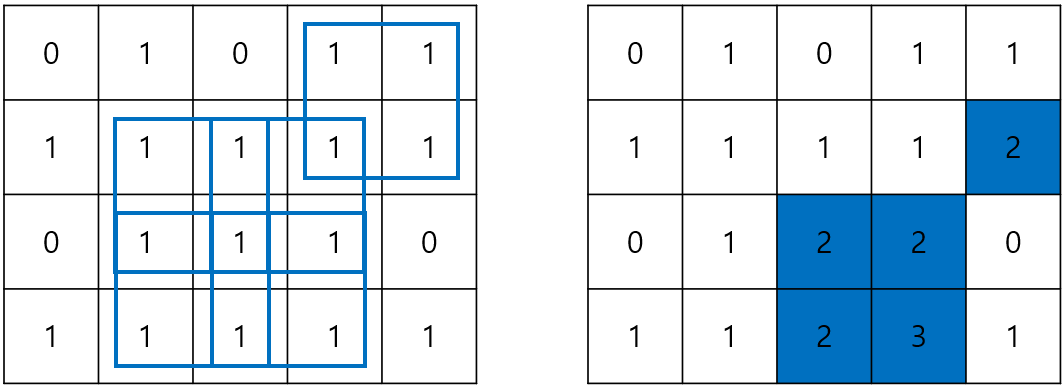
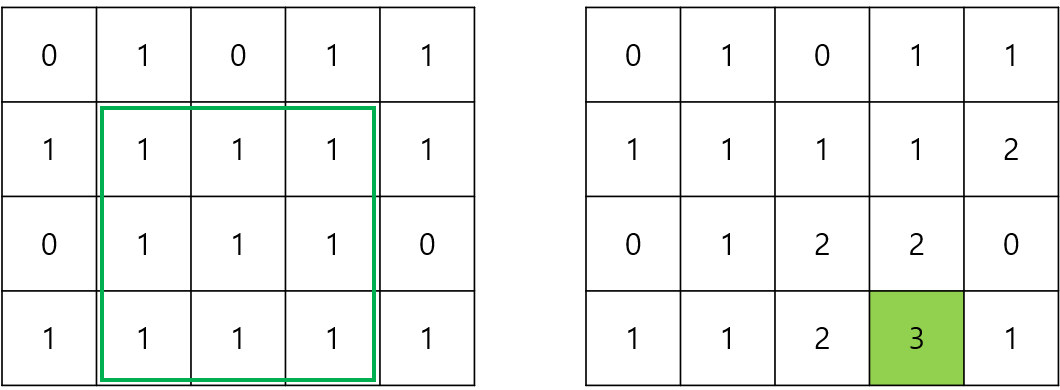
위의 내용을 바탕으로 dp 배열을 채우기 위해서는 4가지 경우를 생각하면 된다.

1. $A_{ij} == 0$ : 이 때에는 정사각형이 만들어질 수 없으므로 dp[i][j] = 0이다.
2. $i == 0$ 또는 $j == 0$ : 이 때에는 만들어질 수 있는 가장 큰 정사각형의 길이가 1이므로 dp[i][j] = 1이다.
3. $A_{i-1j} == 0$ 또는 $A_{ij-1} == 0$ 또는 $A_{i-1j-1} == 0$ : 이 때에는 2 이상의 정사각형을 만들 수 없으므로 dp[i][j] = 1이다.
4. $A_{i-1j} == 1$ 그리고 $A_{ij-1} == 1$ 그리고 $A_{i-1j-1} == 1$ : 이 때에는 2 이상의 정사각형을 만들 수 있으므로 (dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) 중 최솟값에서 1을 더한 값이 dp[i][j]의 값이 된다.

총 4가지 경우로 조건을 나누어 dp 배열을 채워주면 된다.

이 때 4번에서 (dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) 세 값 중 하나에서 0이 있는 경우가 사실 3번과 같은 경우기 때문에 1, 2, 4번 세가지 조건만 따져주어도 같은 결과가 나온다.

dp 배열을 채우면서 최댓값을 계속 갱신해주면 가장 큰 정사각형의 너비 또는 높이를 구할 수 있다.

코드

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

int arr[1001][1001], dp[1001][1001];

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr); cout.tie(nullptr);

    while (1) {
        int N, M; cin >> N >> M;
        if (!N && !M) break;

        memset(arr, 0, sizeof(arr));
        memset(dp, 0, sizeof(dp));
        for (int i = 0; i < N; i++) 
            for (int j = 0; j < M; j++) 
                cin >> arr[i][j];
        
        int mx = 0;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                if (!arr[i][j]) dp[i][j] = 0;
                else if (!i || !j) dp[i][j] = 1;
                else dp[i][j] = min({dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1]}) + 1;
                mx = max(mx, dp[i][j]);
            }
        }

        cout << mx << '\n';
    }
}

후기

처음 구현할 때 1번, 2+3번, 4번 조건으로 나누어서 코드를 구현했는데 글을 쓰다 보니 사실 3번 조건이 4번 조건에서 처리되어 1번, 2번, 4번 조건만으로 충분하다는 것을 알 수 있었다.